
Vsebina
- Zipfov zakon je pojasnil
- Osnovni poskus
- Zipfov zakon na trgih Steam
- Kaj se lahko naučimo o Steamu?
- Sklepi
Pred kratkim je moj prijatelj predlagal, da gledam videoposnetek Vsaucesa o zakonu Zipfa, Paretovem načelu in njihovih skrivnostnih nastopih okoli nas. Tukaj je malo teaser, da pridobi vašo pozornost - 80% vseh ljudi živi v 20% najbolj priljubljenih mest; 80% vseh zemljišč pripada 20% najbogatejših najemodajalcev; 80% vseh odpadkov je na 20% najbolj umazanih ulicah, kot je napovedal Zipfov zakon in načelo Paretos.
Ne dovolj? No, kot sem včeraj odkril, se zajecna luknja tu ne ustavi ... Polna skepticizma, odločila sem se, da pogledam, koliko časa ljudje porabijo za igranje parnih iger ... No. 80% časa se porabi za igranje 20% najbolj priljubljenih iger ... Zanimivo? No, nadaljujte, še več je v tej zgodbi.
Čas je več kot 20 minut, Vsauces si prizadeva za veliko stvari, ki razkrivajo veliko stvari o Zipf-u, vendar je zelo sramežljiv pri prikazovanju osrednjega mehanizma, ki naj bi prispeval k temu, da Zipf deluje tako. Torej, preden gremo naprej, bi rada na kratko to pojasnila.
Zipfov zakon je pojasnil
Obstaja več konceptualnih načinov, kako razložiti intuicijo za načelom 20/80. Najboljši primer, po mojem mnenju, je tisti o lončkih kraterjih.
Osnovni poskus
Predstavljajte si, če boste, da je nedotaknjena Luna - popolnoma gladka površina. Zdaj pa recite, da obstajajo nekaj naključno velikih asteroidov, ki lovijo na Luno. Ko pride prvi asteroid, zapusti krater. Zdaj pa zadene še en krater, drugje. Vsak krater je del celotne površine, zato obstaja možnost, da bo naslednji naključni asteroid zadel blizu obstoječega kraterja in se mu pridružil, tako da bo tvoril skupino. Možnost, da bi novi asteroid zadel določen krater, je potem sorazmerna z obstoječimi velikostmi kraterjev in asteroidov. To pomeni, da se naslednji naključni asteroid bolj verjetno pridruži največji obstoječi skupini, zaradi česar je še večji. Nekakšen kumulativni proces, ki nato ustvari bogati, bogatejši, slabše-dobite-lonije.
Imejte to v mislih, ker je to verjetno splošna razlaga za "zakaj" zakon Zipfs deluje s tako skrivnostno univerzalnostjo. Primer asteroida je dokaj preprost, vendar je vprašanje, kaj se bo zgodilo ob mnogih ponovitvah
Malo zmedeno?
No, jaz sem naredil gif za vožnjo te začetne točke domov. Opomba! o grafu bomo razpravljali kasneje, samo poskusite sliko preizkusiti.

Če opazimo dejansko Luno, se izkaže, da se s povečanjem količine asteroidov do velikih količin premeri kraterja povečajo tako, da 20% največjih kraterjev doseže 80% celotne površine.
Torej, ko gremo na več asteroidov, se distribucija najbolj priljubljenih in najmanj priljubljenih skupin približa nekakšni "idealni distribuciji" s to lastnostjo 20/80 - paretovo porazdelitvijo. Če naredite matematiko, se izkaže, da (na splošno), če ima največja skupina velikost N, je druga največja skupina okoli velikosti N / 2, tretja N / 3 in tako naprej in tako naprej. To se imenuje Zipfov zakon. Čudna stvar je Zipfov zakon in paretova distribucija dela za osupljivo količino elementov (asteroidov) in skupin (grozdov kraterjev). Seveda obstajajo asimetrične in naključne motnje, toda splošni trend je nesporen.
Upam, da lahko vidite, kako je večja verjetnost, da bodo asteroidi udarili v velike kraterje na Luni, da bodo mesta privlačnejša, če v njih že živi več ljudi. Vendar se moramo zavedati, da so mesta daleč od edinih "skupin", ki se obnašajo v skladu z Zipfom.
Tukaj je nekaj primerov iz raziskave Mark Newmans o Pareto distribucijah. Opomba! Grafi so v log-log lestvici, ki izravnava hiperbolično obliko krivulj, kar predstavlja skoraj linearno razmerje.
Začetno y = aX ^ (- b)
Dnevniki obeh strani => log y = log a - b log X
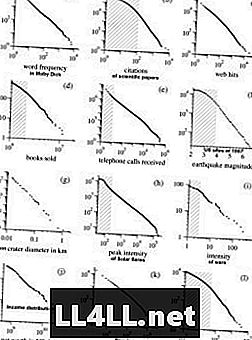
Zanimivo je, da se isti trend kaže tudi v verskih kultih ... Skupna lastnost večine teh pojavov je preprosto ta tendenca »velikih skupin - dobite več«. Tako je Zipfov zakon vztrajal pri mehanizmih, kjer so preference elementov pozitivno povezane z velikostjo skupin (kar pomeni, da ko je skupina večja, verjetneje se bo povečala). Zato rad delam skupine kot grozde in elemente kot skupine grozdov.
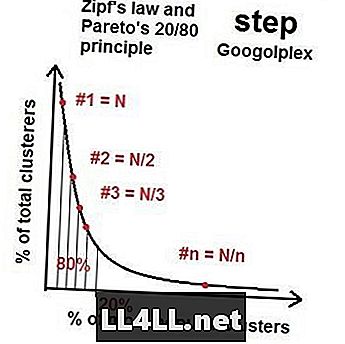
Zipfov zakon na trgih Steam
Sumljivega za to zadnjo? Tukaj je čas, ki ga ljudje porabijo za najbolj priljubljene igre na Steam .. Podatki iz SteamSpy.
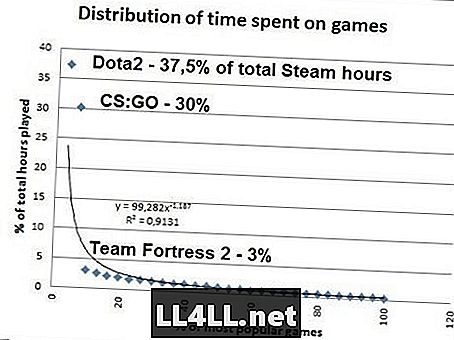
Če naredite matematiko, se izkaže, da 20% najbolj priljubljenih iger na paru predstavlja 80% celotne količine igranja, zato skrivnost Pareto 20/80 deluje tukaj kot čar ... t Zipf je resničen, CS: GO 37,5% / 2 = 18,8% celotnega časa, namesto ogromnih 30%. Ampak, razen tega, da se izognemo (STOP PLAYING) CS: GO), je zipf podobna distribucija očitno tam.
Tukaj je količina prodanih izvodov za najbolj priljubljene igre.
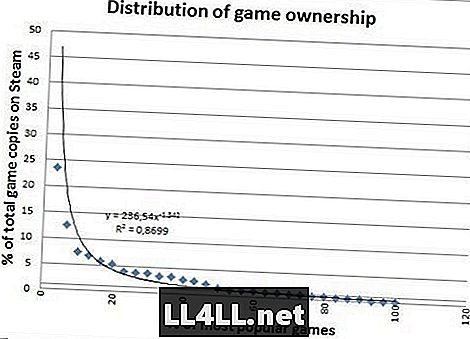
Izgleda lepše eh? Prodajne kopije nimajo velikih odstopanj, zato se zelo dobro prilega, kar je pomembna razlika. Toda iz razlik zadnjih dveh grafov je nekaj bolj zanimivega.
Ali opazite, da je "rep", ki gre na desno, neke vrste maščoba v drugem grafu? Preprosto povedano, to nam pove, da so "relativno nepriljubljene" igre pravzaprav precej bolj priljubljene kot v prejšnji igri.
Pravzaprav se izkaže, da 20% najbolj priljubljenih iger predstavlja samo 60% prodaje, v primerjavi z 80% igranja. Zanimivo? Stavite, da je res.
Kaj se lahko naučimo o Steamu?
No, dejstvo, da popularnost igre sledi Paretovi distribuciji, nam pove, da dejansko obstaja nekakšen pozitivni učinek omrežja, zaradi katerega igralci izberejo igre, ki jih že igra več ljudi. Kakšna je razlika v debelosti repov nam pove, da so uporabniki Steama pri nakupu iger veliko bolj "slepi za velikost skupine", kot so, ko jih igrajo.
Razmislite o tem - čim več ljudi kupi igre, ne glede na "trenutno priljubljeno mnenje", bolj porazdeljena je Paretova distribucija, saj je manj verjetno, da bodo velike igre še naprej rasle. Če nihče ni podkladal podgane o tem, koliko ljudi že igra igro in je razpoložljivost vseh iger enaka, potem pričakujemo, da bo 20% najbolj priljubljenih iger predstavljalo približno 50% prodaje in igranja (npr. Ob predpostavki, da so posamezne preference običajno porazdeljeni).
Sklepi
Tako sta dva dejavnika, ki prispevata k Paretovi distribuciji na trgih Steam - kako inovativni razvijalci (koliko novih lončkov se oblikujejo) in koliko igralci (asteroidi) vrednotijo trenutno velikost skupine, ko izberejo, katera skupina naj se pridruži . Izkazalo se je, da so igralci pri nakupu iger zelo slepi za skupine, toda ravno nasprotno, ko jih igrajo. Hladna huh?
Če želite izvedeti več o Zipfovih distribucijah zakona in zakona, je tukaj lepo predavanje. Poleg tega se prepričajte, da si oglejte Newmanov papir!
Če želite prebrati več o tej vrsti stvari, bom kmalu poskusil združiti to opazovanje z modelom, ki kaže, da imajo bolj priljubljene igre za več igralcev višje cene (ki se povezujejo z željo igralcev, da se pridružijo skupinam večje velikosti). Oglejte si članek tukaj. Članek Piece De Resistance bo združil te teorije in pojasnil, kako so igre za več igralcev, socialna omrežja in mesta dejansko vsi protirakovni izdelki z omrežnimi učinki (več ljudi porabi dobro, več koristi posameznemu potrošniku), ki ima jih je upravljal s to meglo skrivnosti Zipfian ...
Do takrat - uživajte!
P.S. Pojdite v komentar z zabavno idejo za odnos 20/80, za katerega menite, da je lahko res.
Moje so:
80% nostalgije ljudstva povzroča 20% njihovih najsrečnejših spominov (dejansko dokazano za stopnjo, ki jo ljudje pozabljajo)
80% mase je koncentriranih v 20% največjih vesoljskih objektov (dejansko dokazano za porazdelitev gravitacijske sile)
In seveda
80% nereda v vašem WC-ju prihaja iz 20% tega, kar jeste (brez akademskih raziskav)